Editor's note: Jacob Andreas, a senior research scientist at Microsoft Semantic Machines and a PhD in Computer Science from UC Berkeley, took control problems as an example to discuss the idea of ​​introducing planning capabilities into the representation space of reinforcement learning.
Agents that use neural networks as parameters (such as Atari player agents) seem to generally lack the ability to plan. Monte Carlo reactive agents (such as primitive deep Q learners) are obviously an example, and even agents with a certain hidden state (such as the MemN2N paper by NIPS) seem to be the same. Nevertheless, similar planning behaviors have been successfully applied to other deep models, especially in text generation-cluster decoding, and even cluster training, which seems indispensable for machine translation and image description. Of course, for those dealing with control issues that are not at the toy level, real planning issues are everywhere.
Task and movement planning is a good example. Once we needed to solve a continuous control problem, but it was too difficult to solve it directly (through a general control strategy or a TrajOpt-like process). So we turned to a highly simplified, hand-specified problem code—perhaps a STRIPS representation that discarded geometric information. We solved the (relatively simple) STRIPS planning problem, and then projected it back into the motion planning space. This projection may not correspond to a feasible strategy! (But we want to make strategies that are feasible in the task space as feasible as possible in the motion space.) We continue to search the planning space until we find a solution that works in the motion space at the same time.
In fact, this is just a pruning plan from coarse to fine-we need a low-cost method that can discard plans that are obviously infeasible, so that we can concentrate all computing resources on situations that really need to be simulated.
as the picture shows:
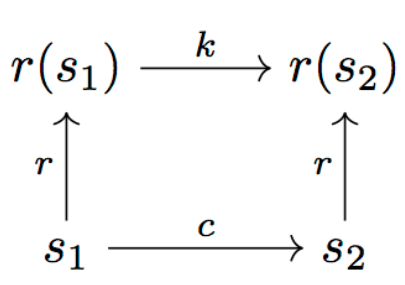
In the above figure, r is the representation function, c is the cost function (we can think of it as a function that uses 0-1 to represent the feasibility judgment), and k is the "representation cost". We want to ensure that r is "close to isomorphism" in motion cost and task cost, that is, c(s1, s2) ≈ k(r(s1), r(s2)).
As far as the STRIPS version is concerned, suppose we give r and k manually. However, can we learn a better representation for solving tasks and motion planning problems than STRIPS?
Learn from planning samples
First, suppose that we already have training data, which is a sequence of successful motion space waypoints (s1, s2, …, s*). Then we can directly minimize the following objective function:
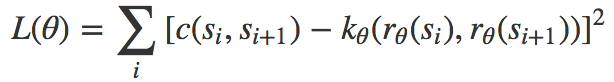
The easiest case is that the representation space (the corresponding domain of r) is â„d; then we can operate d to control the balance between the representation quality and the cost of searching the representation space.
Problem: If we only observe the constant c (this may happen if we only see good solutions), then there is no pressure to learn the less trivial k. So we also need unsuccessful attempts.
decoding
Given the trained model, we solve the new instance through the following steps:
Sample a cost-weighted path (r1, r2, ..., rn) that satisfies r(s*) ≈ rn from the representation space.
Map each representation space transformation r1→r2 to motion space transformation s1→s2, and satisfy r(s2) ≈ r2. (If r is differentiable, then this is easy to express as an optimization problem, otherwise it needs a little trouble to express as a strategy.)
Repeat the above process until the motion space solution of one of them is feasible.
In each step involved in calculating the path (whether in r-space or s-space), we can use a wide range of technologies, including optimization-based technologies (TrajOpt), search-based technologies (RRT, but probably not Applicable to high-dimensional situations), or through learning strategies that take target states as parameters.
Learning directly from task feedback
What if we don’t have a good track to learn from? Just modify the previous two steps-starting from a random initial value, expand the sequence of r and s that contains the prediction, and then generate a sequence of predicted values ​​r and s, and then treat it as supervision, and update k to reflect the observations. To the cost.
Suggestive search
So far, we have assumed that the representation space can be directly brute force searched until we are close to the target. There is no mechanism to force that the proximity of the space is also close to the motion space (except for the smoothness that r may bring). We may want to add additional restrictions. If the distance rn is more than 3 hops by definition, then ||ri−rn||>||ri+1−rn||. This immediately provides a convenient heuristic algorithm for searching in the representation space.
We can also introduce auxiliary information at this stage—perhaps in the form of language or video opinions. (Next we need to learn another mapping from opinion space to representation space.)
Modular
In the field of STRIPS, it is common practice to define some different primitives (such as "mobile" and "crawl"). We may want to provide the agent with a discrete list of similar different strategies. The strategies on the list list conversion costs k1, k2, …. The search problem now involves both (continuously) selecting a set of points and (discretely) selecting a cost function/motion primitive for moving between points. The motion corresponding to these primitives may be limited to a (manually selected) submanifold in the configuration space (for example, only the end effector is moved, and only the first joint is moved).
Thanks to Dylan Hadfield-Menell for the discussion of mission and motion planning.
PC Cable:MINI DIN,D-SUB,SCSI.The display connecting line includes the data cable connecting the host computer and the display screen, and the power cable connecting the power supply.
The common data cable types are: HDMI cable, VGA cable and DVI cable. There is also a DP cable for notebook!
This product is suitable for computer and automatic connection cable with rated voltage of 500V and below. K type B low density polyethylene (LDPE) with oxidation resistance is used for insulation of cable ground wire core. Polyethylene has high insulation resistance, good voltage resistance, small dielectric coefficient and small influence of dielectric loss temperature and variable frequency. It can not only meet the requirements of transmission performance, but also ensure the service life of the cable. One
In order to reduce the mutual crosstalk and external interference between loops, the cable adopts shielding structure. According to different occasions, the shielding requirements of cables are as follows: the combined shielding of twisted pair, the total shielding of cable composed of twisted pair, and the total shielding after the combined shielding of twisted pair.
Shielding materials include round copper wire, copper strip and aluminum / plastic composite belt. Shielding pair and shielding pair have good insulation performance. If there is potential difference between shielding pair and shielding pair, the transmission quality of signal will not be affected.
PC Cable
ShenZhen Antenk Electronics Co,Ltd , https://www.antenk.com